2018/2019 Mathematics Questions and Answers
Question 1
1. Without using tables or calculator, simplify: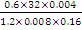 leaving the answer in standard form (scientific notation).
leaving the answer in standard form (scientific notation).
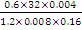 leaving the answer in standard form (scientific notation).
leaving the answer in standard form (scientific notation).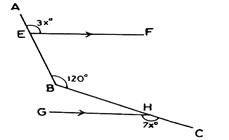
Observation: In the diagram,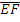 is parallel to
is parallel to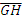 . If ∠AEF = 3xo, ∠ABC = 120o and ∠CHG = 7xo, find the value of ∠GHB.
. If ∠AEF = 3xo, ∠ABC = 120o and ∠CHG = 7xo, find the value of ∠GHB.
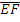 is parallel to
is parallel to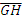 . If ∠AEF = 3xo, ∠ABC = 120o and ∠CHG = 7xo, find the value of ∠GHB.
. If ∠AEF = 3xo, ∠ABC = 120o and ∠CHG = 7xo, find the value of ∠GHB.
The Chief Examiner reported that this question was attempted by majority of the candidates and they performed better in part (a) than in part (b). However, it was also reported that while some of the candidates were able to simplify the fraction in part (a), they did not express the solution in standard form as required.
In part (a), majority of the candidates were reported to have multiplied both the numerator and the denominator of the fraction by 106 to obtain:
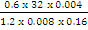 x
x 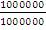 =
= 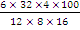 =
= 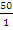 = 5 x 101
= 5 x 101
In part (b), majority of the candidates were reported not to have gotten the question right. Candidates were expected to construct a line parallel to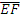 and passing through B or produce line AB to meet GH. This would have led them to obtain the equation
and passing through B or produce line AB to meet GH. This would have led them to obtain the equation
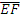 and passing through B or produce line AB to meet GH. This would have led them to obtain the equation
and passing through B or produce line AB to meet GH. This would have led them to obtain the equation
3xo + 180o – 7xo =1200. Solving this equation gave xo=15o. Therefore angle GHB would be 180o – 7(15o) =750.
Question 2
1.Simply 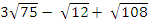 , leaving the answer in surd form (radicals)
, leaving the answer in surd form (radicals)
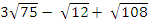 , leaving the answer in surd form (radicals)
, leaving the answer in surd form (radicals)
2.If 124n= 232five, find.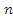
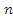
Observation: The Chief Examiner reported that this was the most attempted question and majority of the candidates obtained full marks. Their performance was commended by the Chief Examiner.
In part (a), candidates were reportedly able to simplify 3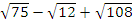 to have
to have 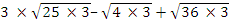 which further simplified to 15
which further simplified to 15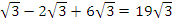 .
.
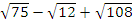 to have
to have 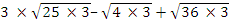 which further simplified to 15
which further simplified to 15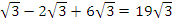 .
.
In part (b), majority of the candidates were also reported to have converted both sides of the sign of equality to base 10 and then compared them. That is, 124n 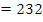 fiveconverted to base 10 gave (1
fiveconverted to base 10 gave (1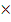 n2)
n2)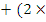 n1)
n1) 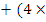 n0)
n0)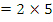 2
2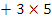 1
1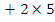 0. Simplifying the equation and bringing likes terms together gave n2 + 2n – 63 = 0. Solving this quadratic equation gave n = 7. The other value for n, which was -9, was not acceptable because it was negative.
0. Simplifying the equation and bringing likes terms together gave n2 + 2n – 63 = 0. Solving this quadratic equation gave n = 7. The other value for n, which was -9, was not acceptable because it was negative.
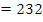 fiveconverted to base 10 gave (1
fiveconverted to base 10 gave (1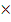 n2)
n2)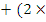 n1)
n1) 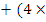 n0)
n0)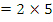 2
2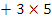 1
1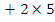 0. Simplifying the equation and bringing likes terms together gave n2 + 2n – 63 = 0. Solving this quadratic equation gave n = 7. The other value for n, which was -9, was not acceptable because it was negative.
0. Simplifying the equation and bringing likes terms together gave n2 + 2n – 63 = 0. Solving this quadratic equation gave n = 7. The other value for n, which was -9, was not acceptable because it was negative.
Question 3
1. Solve the simultaneous equations:
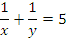
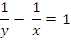
A man drives from Ibadan to Oyo, a distance of 48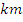 in 45 minutes. If he drives at 72
in 45 minutes. If he drives at 72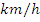 where the surface is good and 48
where the surface is good and 48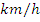 where it is bad, find the number of kilometers of good surface.
where it is bad, find the number of kilometers of good surface.
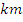 in 45 minutes. If he drives at 72
in 45 minutes. If he drives at 72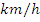 where the surface is good and 48
where the surface is good and 48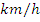 where it is bad, find the number of kilometers of good surface.
where it is bad, find the number of kilometers of good surface.
Observation: The Chief Examiner reported that this question was popular among the candidates but while majority of them were able to attempt part(a) successfully, majority of them performed poorly in part (b).
In part (a), candidates were expected to apply the elimination method to solve the simultaneous equations. Adding both equations gave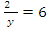 which implied that
which implied that 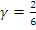 =
=  Subtracting the two equations gave
Subtracting the two equations gave 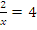 . This implied that
. This implied that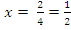 . Hence
. Hence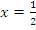 , and y =
, and y = 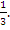
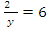 which implied that
which implied that 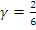 =
=  Subtracting the two equations gave
Subtracting the two equations gave 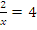 . This implied that
. This implied that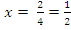 . Hence
. Hence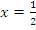 , and y =
, and y = 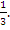
In part (b), candidates were reported not to translate the word problem into mathematical expression correctly. Teachers were encouraged to emphasize this area of the syllabus during instruction. Candidates were expected to show that if 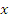 was the number of kilometers of good surface, then using the formula,time
was the number of kilometers of good surface, then using the formula,time 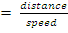 ,
,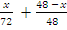 = 45 minutes =
= 45 minutes = 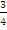 hours. Solving this equation gave x = 36 km.
hours. Solving this equation gave x = 36 km.
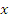 was the number of kilometers of good surface, then using the formula,time
was the number of kilometers of good surface, then using the formula,time 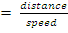 ,
,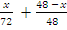 = 45 minutes =
= 45 minutes = 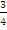 hours. Solving this equation gave x = 36 km.
hours. Solving this equation gave x = 36 km.
Question 4
1.(a)
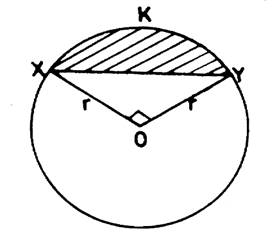
In the diagram, O is the centre of the circle radius 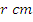 and ∠
and ∠ 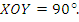 If the area of the shaded part is 504
If the area of the shaded part is 504 2, calculate the value of
2, calculate the value of 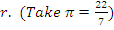
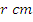 and ∠
and ∠ 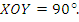 If the area of the shaded part is 504
If the area of the shaded part is 504 2, calculate the value of
2, calculate the value of 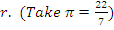
(b) Two isosceles triangles 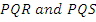 are drawn on opposite sides of a common base PQ. If ∠,
are drawn on opposite sides of a common base PQ. If ∠, 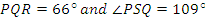 calculate the value of ∠
calculate the value of ∠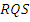 .
.
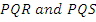 are drawn on opposite sides of a common base PQ. If ∠,
are drawn on opposite sides of a common base PQ. If ∠, 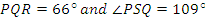 calculate the value of ∠
calculate the value of ∠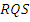 .
.
Observation: This question was also reported to have been attempted by majority of the candidates and their performance was described as fair.
In part (a), a good number of the candidates were reported not to apply the correct formula. Others who were able to apply the formula correctly were reported not to simplify correctly. Candidates were expected to recognize the shaded portion as a segment of a circle. The area of the shaded portion would be gotten by subtracting the area of triangle O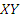 from the area of sector OXKY. Area of triangle OXY=
from the area of sector OXKY. Area of triangle OXY=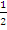 r2sin90o=
r2sin90o=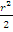 . Area of sector OXKY
. Area of sector OXKY 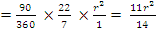 . Area of shaded portion
. Area of shaded portion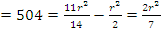 . Solving this equation gave r
. Solving this equation gave r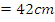 .
.
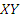 from the area of sector OXKY. Area of triangle OXY=
from the area of sector OXKY. Area of triangle OXY=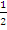 r2sin90o=
r2sin90o=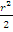 . Area of sector OXKY
. Area of sector OXKY 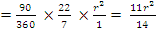 . Area of shaded portion
. Area of shaded portion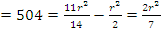 . Solving this equation gave r
. Solving this equation gave r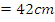 .
.
In part (b), majority of the candidates were reported not to draw the required diagram correctly and this affected their ability to solve the question correctly. The expected diagram was
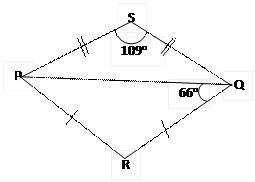
From the diagram, angle SQR =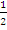 (180 -109)0
(180 -109)0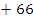 0
0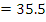 0
0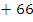 0
0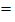 101.50
101.50
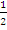 (180 -109)0
(180 -109)0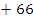 0
0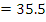 0
0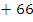 0
0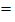 101.50
101.50
Question 5
A building contractor tendered for two independent contracts, X and Y. The probabilities that he will win contract X is 0.5 and not win contract Y is 0.3. What is the probability that he will win:
both contract;
exactly one of the contracts;
neitherof the contracts?
Observation: This question was reported to be attempted by majority of the candidates and they performed very well in it. It was one question where candidates were reported to have shown significant strength as majority of them scored full marks.
Candidates were reported to show that if the probability of winning contract X,P(X)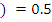 , then the probability of not winning contract X, P(X’) = 1 – P(X) = 1 -
, then the probability of not winning contract X, P(X’) = 1 – P(X) = 1 -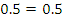 . Similarly, if the probability of not winning contract Y, P(Y’)
. Similarly, if the probability of not winning contract Y, P(Y’) 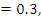 the probability of winning contract Y, P(Y) = 1 – P(Y’)
the probability of winning contract Y, P(Y) = 1 – P(Y’) 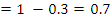 . Probability of winning both contracts was given by P(X)
. Probability of winning both contracts was given by P(X) 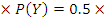 0.7
0.7 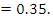 Probability of winning exactly one contract = Probability of (winning X and not winning Y) or (not winning X and winning Y) = (
Probability of winning exactly one contract = Probability of (winning X and not winning Y) or (not winning X and winning Y) = ( 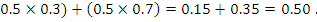 Probability of wining neither contract = Probability of not winning X and Y =
Probability of wining neither contract = Probability of not winning X and Y =  .
.
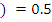 , then the probability of not winning contract X, P(X’) = 1 – P(X) = 1 -
, then the probability of not winning contract X, P(X’) = 1 – P(X) = 1 -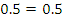 . Similarly, if the probability of not winning contract Y, P(Y’)
. Similarly, if the probability of not winning contract Y, P(Y’) 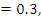 the probability of winning contract Y, P(Y) = 1 – P(Y’)
the probability of winning contract Y, P(Y) = 1 – P(Y’) 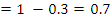 . Probability of winning both contracts was given by P(X)
. Probability of winning both contracts was given by P(X) 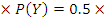 0.7
0.7 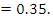 Probability of winning exactly one contract = Probability of (winning X and not winning Y) or (not winning X and winning Y) = (
Probability of winning exactly one contract = Probability of (winning X and not winning Y) or (not winning X and winning Y) = ( 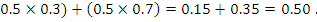 Probability of wining neither contract = Probability of not winning X and Y =
Probability of wining neither contract = Probability of not winning X and Y =
Question 6
1.If 
2.A television set was marked for sale at in order to make a profit of 20. The television set was actually sold at a discount of 5 Calculate, correct to 2 significant figures, the actual percentage profit.
in order to make a profit of 20. The television set was actually sold at a discount of 5 Calculate, correct to 2 significant figures, the actual percentage profit.
Observation: The Chief Examiner reported that Candidates’performance on this question was poor. Majority of the candidates were reported to exhibit poor manipulative skills on the problem involving fractions. The problem on Commercial arithmetic was also reported to be poorly attempted by majority of the candidates.
In part (a), candidates were expected to cross multiply both sides of the sign of equality to obtain . Multiplying through by the LCM which was 12 gave
. Multiplying through by the LCM which was 12 gave . Bringing like terms together and simplifying gave
. Bringing like terms together and simplifying gave .
.
In part (b) candidates were expected to obtain the cost price of the television set using the formula
Percentage profit . That is,
. That is, . Solving this equation gave
. Solving this equation gave  Actual selling price was 95% of 760 i e
Actual selling price was 95% of 760 i e  Therefore actual percentage profit
Therefore actual percentage profit
Question 7
1. Copy and compete the table of values for the relation
x 









y 1.0 2.7 0.0 -0.7
1. Using scales of  on the
on the axis and 2
axis and 2  unit on
unit on  the axis, draw the graph of
the axis, draw the graph of 
2. Use the graph to find the values of for which
of for which 
Observation: The Chief Examiner reported that majority of the Candidates attempted this question. The report further stated that while majority of them were able to complete the table and draw the graph, they could not obtain the value of x for which .Candidates were encouraged to work harder in this aspect. They were expected to obtain the following table of values
.Candidates were encouraged to work harder in this aspect. They were expected to obtain the following table of values
x 









y 1.0 2.0 2.7 3.0 2.7 2.0 1.0 0.0 

Using these values and the given scales, they were to draw the graph as shown:
Candidates would now find the value of x for which using the graph as follows:
using the graph as follows: . This implied that 2
. This implied that 2 . 2
. 2 or 1.5 Therefore, the line
or 1.5 Therefore, the line would be traced to intersect with the graph.
would be traced to intersect with the graph.
The x – coordinates of the points of intersection of the graph and the line y = 1.5 gave the required solution which was 
Question 8
1. Copy and complete the following table for multiplication modulo 11.
1 1 5 9 10
5 5
9 9
10 10
Use the table to:
1. 

 evaluate (9 5 ) (10 10)
evaluate (9 5 ) (10 10)
2. find the truth set of
3.  10 m=2,
10 m=2,
4. n n = 4
n n = 4
5. When a fraction is reduced to its lowest term, it is equal to . The numerator of the fraction when doubled would be 34 greater than the denominator. Find the fraction.
. The numerator of the fraction when doubled would be 34 greater than the denominator. Find the fraction.
Observation: It was reported that part (a) of this question was poorly attempted by majority of the candidates who attempted it. The Chief Examiner opined that this may be due to the fact that the topic was newly introduced into the curriculum for General Mathematics.
Candidates were expected to complete the table by multiplying the figures, divide the result by 11 and record the remainder to obtain:
1 1 5 9 10
5 5 3 1 6
9 9 1 4 2
10 10 6 2 1
10 x m = 2 was {9}. The number that would multiply itself to have 4 is 9. Therefore the truth set of n x n = 4 was .
.
It was also reported that some of the candidates who were able to solve the question did not express them as sets.
In part (b), the Chief Examiner observed that more work needed to be done by both teachers and candidates in solving word problems. Majority of the candidates were reported not to solve this problem correctly. According to the report, while some of them
could obtain the first equation, majority of them could not obtain the second equation. The few of them who were able to obtain 51 and 68 failed to express the answer as a fraction. Candidates were expected to show that if was the fraction, then from the first statement, =
= . i.e. 4x = 3y -------- eqn.(1). From the second statement, 2x = y + 34 or y = 2x – 34 --------eqn. (2). Substituting 2x – 34 for y in eqn. (1) gave
. i.e. 4x = 3y -------- eqn.(1). From the second statement, 2x = y + 34 or y = 2x – 34 --------eqn. (2). Substituting 2x – 34 for y in eqn. (1) gave
4x = 3(2x – 34). Solving this equation gave x = 51. Substituting 51 for x in eqn. (2) gave y = 68. Therefore the fraction was  .
.
Question 9
U
Inthe Venn diagram, P, Q and R are subsets of the universal set U.
If n(U) = 125, find:
the value of x;
n(PÈQÇR’)
b) In the diagram, O is the centre of the circle. If WX is parallel to YZ and ∠WXY = 50o, find the value of:
∠WXZ;
∠YEZ.
Observation: The Chief Examiner reported that part (a) of this question was attempted by majority of the candidates and they performed well in it. Their performance was reported to be better in part (a) than in part (b) which majority of them did not attempt.
In part (a), majority of the candidates were reported to have added the elements in the universal set,(U), and equated it to 125 to obtain  .Solving this equation gave
.Solving this equation gave .Number of elements in
.Number of elements in  1,
1, n1)
n1) , . Some candidates were reported not to add 4 which was outside the three intersecting sets and this give them a wrong value of x . Others were also reported not to have understood R1, the compliment of R.
, . Some candidates were reported not to add 4 which was outside the three intersecting sets and this give them a wrong value of x . Others were also reported not to have understood R1, the compliment of R.
In part (b), candidates were reported to have exhibited poor knowledge of circle theorems. They were expected to respond as follows:-
Question 10
1. Solve: ( x – 2)(x – 3) = 12
(b)
Observation: In the diagram, M and N are the centres of two circles of equal radii 7 cm. The circles intercept at P and Q. If ∠PMQ = ∠PNQ = 60o, calculate, correct to the nearest whole number, the area of the shaded portion. [ Take
Part (a) of this question was reported to be well attempted by majority of the candidates. They were reported to have correctly expanded the bracket and simplified to obtain 2
2  Solving this quadratic equation gave
Solving this quadratic equation gave  .
.
In part (b), majority of the candidates were reported not to attempt the question. Most of them answered only part (a). The performance of majority of those who attempted it was also reported to be poor. Majority of the candidates were reported not to have recognized the shaded area as two segments from the two circles. Candidates were expected to obtain the area of the segment in each circle and add them. Since the circles were equal, they would only obtain the area for one and multiply it by 2 to obtain the area of the shaded portion as follows
Area of sector cm2 or 25.667cm2.
cm2 or 25.667cm2.
Area of triangle NPQ=  2
2 2 or
2 or  cm2. Therefore, area of shaded portion
cm2. Therefore, area of shaded portion 2
2 2)
2) 2, correct to the nearest whole number.
2, correct to the nearest whole number.
